Was ist der Zinseszinseffekt? Berechnung & Beispiel

Bei der Geldanlage gibt es ein faszinierendes Prinzip, das wie ein unsichtbarer Motor dafür sorgt, dass Kapital immer schneller wächst: der sogenannte Zinseszinseffekt. So kann selbst aus kleinen Beträgen im Laufe der Zeit ein beachtliches Vermögen entstehen. Wie es funktioniert, zeigt der folgende Ratgeber.

Was ist der Zinseszinseffekt?

Bei einer normalen Verzinsung erhält man Zinsen nur auf den ursprünglichen Anlagebetrag. Beim Zinseszins werden die Erträge wieder mit angelegt, wodurch sie selbst neue Zinsen abwerfen. Das lässt dein Vermögen mit der Zeit deutlich schneller wachsen. Je länger die Laufzeit, desto stärker zeigt sich der sogenannte Zinseszinseffekt. Stell dir vor, du legst Geld an und lässt es einfach für dich arbeiten. Die Zinsen, die du bekommst, nimmst du nicht heraus, sondern lässt sie im Topf, sodass sie jetzt selbst Zinsen abwerfen. Mit jedem Jahr wächst so nicht nur dein Kapital, sondern auch die Summe, auf die Erträge berechnet werden. Aus einem kleinen Anfangsbetrag wird mit der Zeit ein stattliches Vermögen, ohne dass man ständig neues Geld einzahlen muss.

Welche Faktoren beeinflussen den Zinseszinseffekt?

Der Zinseszinseffekt ist einer der stärksten Hebel beim langfristigen Vermögensaufbau. Wie stark er wirkt, hängt von mehreren Faktoren ab, die das Wachstum des Kapitals beeinflussen:

• Zinssatz: Je höher der Zins, desto stärker der Effekt.
• Laufzeit: Lange Anlagezeiträume verstärken ihn zusätzlich.
• Zinsgutschriften: Monatliche oder vierteljährliche Zinsgutschriften beschleunigen den Kapitalaufbau im Vergleich zur jährlichen Verzinsung.
• Wiederanlagequote: Nur wenn Erträge vollständig reinvestiert werden, kann der volle Effekt wirken.

Wie berechnet man den Zinseszins?

Der Zinseszins mag auf den ersten Blick kompliziert erscheinen, ist jedoch simple Mathematik. Mit einer einfachen Formel lässt sich berechnen, wie sich das Geld vermehrt, wenn man die Zinsen wieder mit anlegt. Je häufiger eine Gutschrift erfolgt, z.B. monatlich statt jährlich, desto stärker wirkt der Zinseszinseffekt. Im folgenden Beispiel wird das Endkapital bei jährlicher Zinsgutschrift ermittelt.

Hierbei steht:

• K für das Endkapital (Endbetrag mit Zinsen)
• K0​ für das Anfangskapital (z. B. 1.000 €)
• p für den Zinssatz pro Jahr (dezimal, z. B. 5 % = 0,05)
• t für die Laufzeit in Jahren

Zinseszinseffekt: Berechnung mit Beispiel

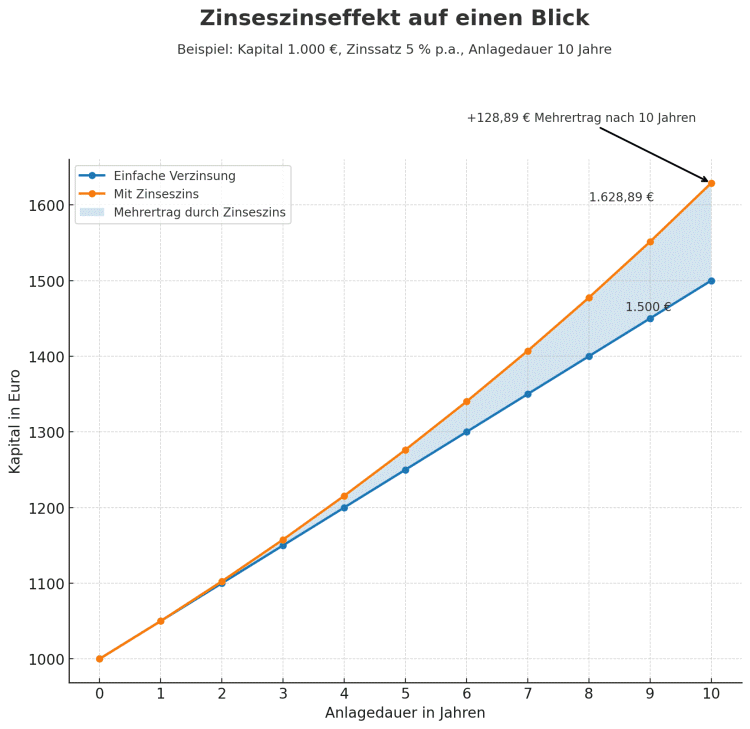
Schauen wir uns das Ganze nun an einem konkreten Beispiel an. Hierfür werden die entsprechenden Zahlen in die Formel eingesetzt. Angenommen, man investiert 1.000 Euro zu einem jährlichen Zinssatz von 5 % für 10 Jahre. Die Zinsgutschrift erfolgt jährlich. Es werden keine weiteren Einzahlungen oder Abhebungen vorgenommen. Die Berechnung würde wie folgt aussehen:

Die anfänglichen 1.000 € sind auf 1.628,89 € angewachsen. Der Zinseszins hat also hier zusätzliche 628,89 € eingebracht.

Berechnung der Rendite ohne Zinseszins

Die folgende Formel berechnet das Endkapital, nur diesmal mit jährlicher Auszahlung, also ohne Zinseszinsen. Wie im obigen Beispiel werden 1.000 € zu 5 Prozent für 10 Jahre angelegt.

Hierbei steht wie oben:

• K für das Endkapital
• K0​ für das Anfangskapital (z. B. 1.000 €)
• p für den Zinssatz pro Jahr (dezimal, z. B. 5 % = 0,05)
• t für die Laufzeit in Jahren

Auch hier wird die Formel wieder mit den entsprechenden Zahlen bestückt. Die Endsumme beträgt 1.500 €, davon entfallen lediglich 500 € auf die Zinsen.

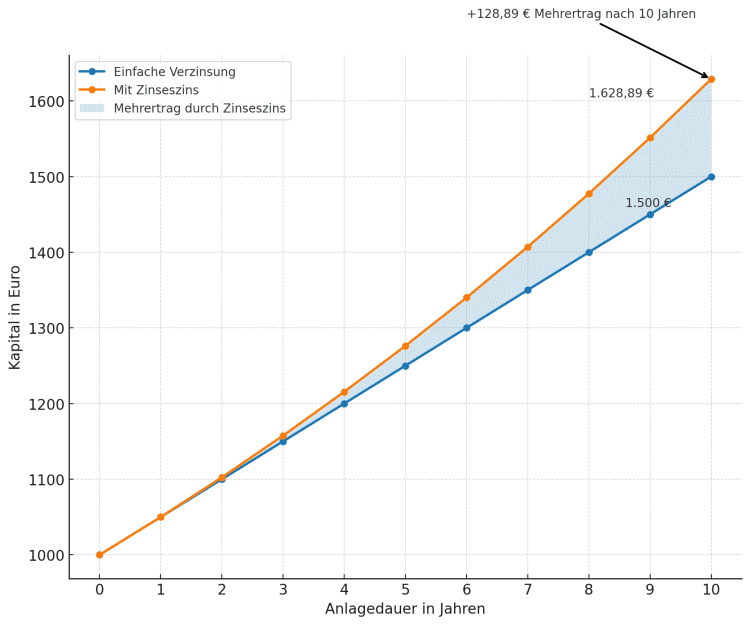
Vergleich: Zinsertrag mit und ohne Zinseszinseffekt

Bei der einfachen Verzinsung bleibt der Ertrag jedes Jahr konstant, während der Zinseszinseffekt dafür sorgt, dass auch die Zinsen selbst wieder Erträge bringen. Der direkte Vergleich zeigt: Über zehn Jahre macht das einen spürbaren Unterschied beim Endkapital.

Der Zinseszins bei vermögenswirksamen Leistungen

Die Auswirkungen des Zinseszinseffekts auf die Rendite zeigt sich besonders bei einer langfristigen Geldanlage wie z.B. den vermögenswirksamen Leistungen. Speziell bei gut verzinsten Sparplänen wie z.B. Fonds oder ETFs profitiert der Anleger vom schnellen Wachstum. Bei VL sind jedoch mehrere Faktoren zu berücksichtigen, wie z.B. die monatliche Sparrate, die durchschnittliche jährliche Rendite, die Gesamtlaufzeit sowie die um 1 Jahr kürzere Einzahlungsdauer.

Berechnung mit Beispiel

Ein Arbeitgeber zahlt seinem Arbeitnehmer 40 € pro Monat. Wie bei VL üblich beträgt die Laufzeit 7 Jahre. 6 davon wird angespart, im siebten Jahr ruht das Kapital. Jede einzelne Rate wird also bis zum Ende des 7. Jahres verzinst. Die durchschnittliche jährliche Rendite beträgt 5 Prozent. Die Verzinsung kann durch die Anpassung der Formel für die zukünftige Wertentwicklung regelmäßiger Einzahlungen sowie die Einführung monatlicher Zinsperioden berechnet werden.

Hierbei steht:

• K für das Endkapital
• R für die monatliche Rate (hier: 40 €)
• p für den Zinssatz pro Jahr (dezimal, z. B. 5 % = 0,05)
• 12 = monatliche Zinsperioden
• Einzahlungen: 72 Monate (Jahr 1 – 6), Verzinsung: 84 Monate (Jahr 1 – 7)

Nun werden wieder die entsprechenden Werte eingesetzt. Die Einzahlungen über die gesamte Dauer betragen: 72 ⋅ 40 = 2.880 €. Das Endkapital beträgt 3.521,99 €. Es wurden somit Zinsen in Höhe von 641,99 € erwirtschaftet (3.521,99 − 2.880 = 641,99).

Kapitalwachstum verschiedener VL-Anlagen

Die folgende Tabelle zeigt, wie sich unterschiedliche Anlageformen für vermögenswirksame Leistungen über die Jahre entwickeln und wie stark der Zinseszins zum Wachstum beiträgt. Grundlage sind durchschnittliche Zinssätze, die aus einer Analyse der Renditen verschiedener Sparprodukte ermittelt wurden. Der Arbeitnehmer zahlt jeweils monatlich 40 € in den Sparvertrag ein. Die Laufzeit beträgt wie bei VL üblich 7 Jahre, von denen 6 aktiv gespart wird. Das Kapital wird jedoch auch im letzten Jahr weiter verzinst. Bei Bausparverträgen wird in der Regel die vollen 7 Jahre eingezahlt. Dieser Unterschied bleibt hier jedoch zugunsten einer besseren Vergleichbarkeit unberücksichtigt.